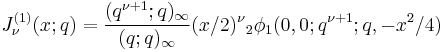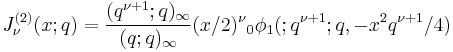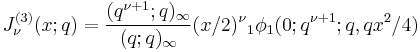Jackson q-Bessel function

In mathematics, a Jackson q-Bessel function (or basic Bessel function) is one of the three q-analogs of the Bessel function introduced by Jackson (1903, 1903b, 1905, 1905b). The third Jackson q-Bessel function is the same as the Hahn–Exton q-Bessel function.

Definition

The three Jackson q-Bessel functions are given in terms of the Pochhammer symbol and the basic hypergeometric function φ by

$J_\nu^{(1)}(x;q) = \frac{(q^{\nu%2B1};q)_\infty}{(q;q)_\infty} (x/2)^\nu {}_2\phi_1(0,0;q^{\nu%2B1};q,-x^2/4)$

$J_\nu^{(2)}(x;q) = \frac{(q^{\nu%2B1};q)_\infty}{(q;q)_\infty} (x/2)^\nu {}_0\phi_1(;q^{\nu%2B1};q,-x^2q^{\nu %2B1}/4)$

$J_\nu^{(3)}(x;q) = \frac{(q^{\nu%2B1};q)_\infty}{(q;q)_\infty} (x/2)^\nu {}_1\phi_1(0;q^{\nu%2B1};q,qx^2/4)$

Ismail, Mourad E. H. (1982), "The zeros of basic Bessel functions, the functions J_{ν +ax}(x), and associated orthogonal polynomials", Journal of Mathematical Analysis and Applications 86 (1): 1–19, doi:10.1016/0022-247X(82)90248-7, ISSN 0022-247X, MR 649849
Jackson, F. H. (1903), "On generalized functions of Legendre and Bessel", Trans. Roy. Soc. Edinburgh 41: 1–28
Jackson, F. H. (1903), "Theorems relating to a generalization of the Bessel functions", Trans. Roy. Soc. Edinburgh 41: 105–118
Jackson, F. H. (1904), "Theorems relating to a generalization of Bessel's function.", Edinb. Roy. Soc. Trans. 41: 399–408, JFM 36.0513.02
Jackson, F. H. (1905), "The Application of Basic Numbers to Bessel's and Legendre's Functions", Proc. London Math. Soc. 2 (1): 192–220, doi:10.1112/plms/s2-2.1.192
Jackson, F. H. (1905), "The Application of Basic Numbers to Bessel's and Legendre's Functions (Second paper)", Proc. London Math. Soc. 3 (1): 1–23, doi:10.1112/plms/s2-3.1.1